Thuật toán Radix Sort trong JavaScript: Sắp xếp dữ liệu hiệu quả và nhanh chóng

Trong thế giới số hóa hiện nay, việc sắp xếp dữ liệu là một phần quan trọng trong lĩnh vực lập trình. Có nhiều thuật toán sắp xếp phổ biến, và mỗi thuật toán đều có những ưu điểm và hạn chế riêng. Trong bài viết này của Tuấn Anh UET, chúng ta sẽ tìm hiểu về thuật toán Radix Sort – một trong những thuật toán sắp xếp độc đáo và hiệu quả trong JavaScript.

Radix Sort được thiết kế để xử lý các số nguyên hoặc chuỗi dữ liệu và có thể sắp xếp chúng theo từng chữ số. Điều này giúp thuật toán thực hiện tốt hơn với các tập dữ liệu lớn và giúp tối ưu hóa hiệu suất trong các ứng dụng thời gian thực. Bạn sẽ tìm hiểu cách hoạt động của thuật toán, triển khai nó trong JavaScript, và nhận thấy lý do tại sao Radix Sort đang HOT trong cộng đồng lập trình thời gian gần đây.

I. Cách hoạt động của thuật toán Radix Sort

A. Đặc điểm cơ bản của thuật toán Radix Sort

1. Radix Sort là một thuật toán sắp xếp phi tuyến tính, được sử dụng để sắp xếp các số nguyên không âm.
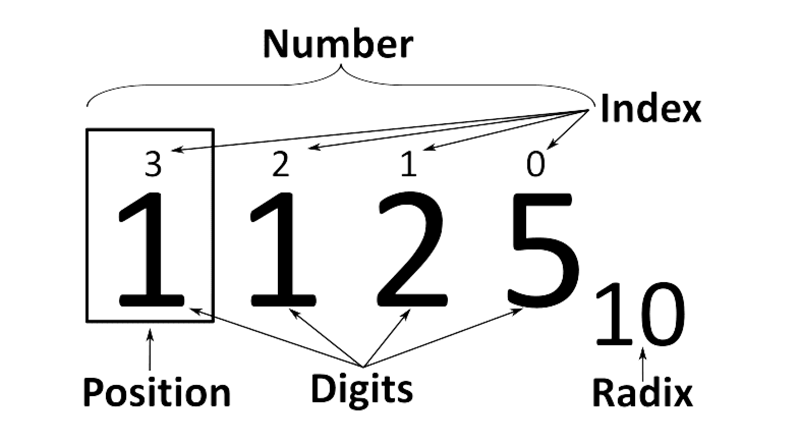
2. Thuật toán Radix Sort dựa trên việc sắp xếp dữ liệu theo từng chữ số từ trái sang phải (Least Significant Digit) hoặc từ phải sang trái (Most Significant Digit).
3. Đặc điểm đáng chú ý của Radix Sort là không sử dụng so sánh trực tiếp giữa các phần tử, thay vào đó nó dựa vào việc phân loại các phần tử vào các “thùng” (buckets) tương ứng với giá trị của chữ số hiện tại.

B. Cách sắp xếp dữ liệu theo từng chữ số (Least Significant Digit) và từng chữ số (Most Significant Digit)

Least Significant Digit (LSD) Radix Sort

1. Bắt đầu từ chữ số thấp nhất (vị trí phải nhất) của các số.
2. Phân loại các số vào các thùng tương ứng với giá trị của chữ số này.
3. Sắp xếp các số theo thứ tự của thùng từ trái sang phải.
4. Lặp lại quá trình trên với chữ số tiếp theo (từ phải sang trái) cho đến khi sắp xếp xong tất cả các chữ số.

Most Significant Digit (MSD) Radix Sort

1. Bắt đầu từ chữ số cao nhất (vị trí trái nhất) của các số.
2. Phân loại các số vào các thùng tương ứng với giá trị của chữ số này.
3. Sắp xếp các số theo thứ tự của thùng từ trái sang phải.
4. Lặp lại quá trình trên với chữ số tiếp theo (từ trái sang phải) cho đến khi sắp xếp xong tất cả các chữ số.

C. Phân tích hiệu suất và độ phức tạp của thuật toán

1. Độ phức tạp thời gian của Radix Sort là O(d * (n + k)), trong đó d là số chữ số của số lớn nhất, n là số lượng phần tử và k là số lượng các giá trị khả dĩ của một chữ số (thường là 10).
2. Radix Sort thường được sử dụng trong trường hợp số lượng phần tử n lớn và giá trị của d không quá lớn, để đảm bảo hiệu suất tốt hơn so với các thuật toán sắp xếp so sánh truyền thống như QuickSort hoặc MergeSort.
3. Tuy nhiên, khi số lượng phần tử n nhỏ hoặc giá trị của d rất lớn, Radix Sort có thể trở nên không hiệu quả và không phù hợp.

Có thể bạn quan tâm: TOP 3 phần mềm giả lập Java tốt nhất và HOT nhất trên Android

II. Triển khai thuật toán Radix Sort trong JavaScript

A. Mô tả giải thuật và quy trình sắp xếp dữ liệu

Thuật toán Radix Sort được triển khai dựa trên việc sắp xếp dữ liệu theo từng chữ số từ phải sang trái (Most Significant Digit – MSD) hoặc từ trái sang phải (Least Significant Digit – LSD). Quy trình sắp xếp dữ liệu như sau:

1. Đầu tiên, xác định số lượng chữ số của số lớn nhất trong dãy số và lưu vào biến “maxDigits”.
2. Với mỗi chữ số từ phải sang trái hoặc từ trái sang phải, thực hiện các bước sau:
3. a. Tạo một mảng các “thùng” (buckets) để phân loại các số vào theo giá trị của chữ số hiện tại.
4. b. Đặt các số vào thùng tương ứng với chữ số hiện tại.
5. c. Gộp các thùng lại thành một dãy số mới theo thứ tự từ trái sang phải hoặc từ phải sang trái.

B. Code mẫu của thuật toán Radix Sort trong JavaScript

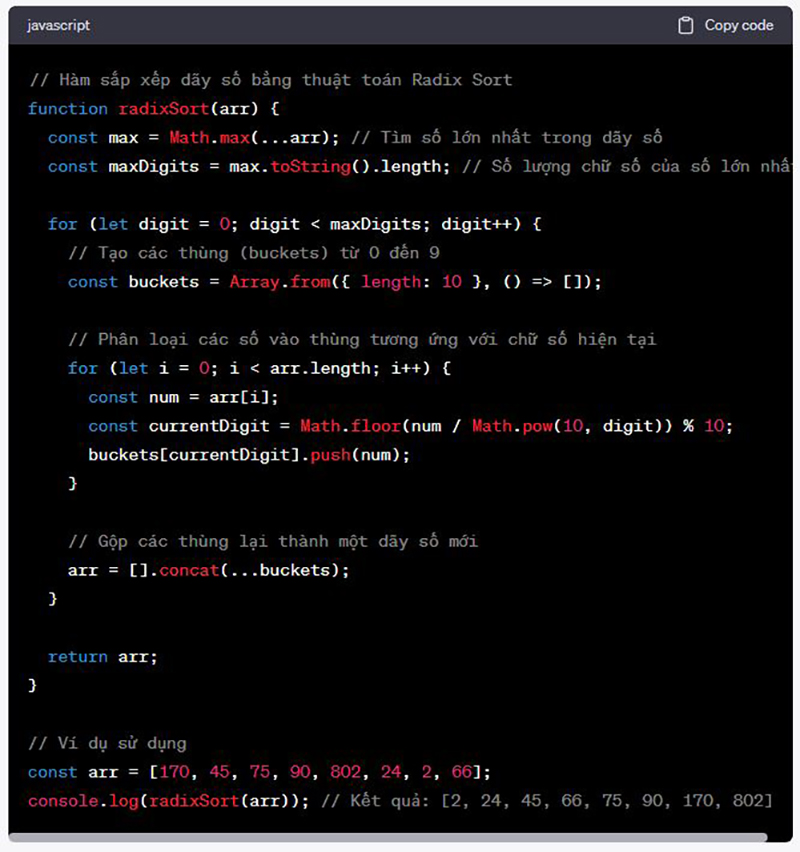
C. Kiểm tra và đánh giá hiệu quả của thuật toán trên các tập dữ liệu khác nhau

1. Radix Sort có hiệu quả tốt đối với các tập dữ liệu có kích thước lớn và giá trị chữ số không quá lớn.
2. Tuy nhiên, trên các tập dữ liệu nhỏ hoặc các giá trị chữ số rất lớn, hiệu quả của Radix Sort có thể bị giảm xuống, và trong trường hợp này, các thuật toán sắp xếp so sánh như QuickSort hoặc MergeSort có thể hiệu quả hơn.

III. Ưu điểm và hạn chế của thuật toán Radix Sort

A. Ưu điểm của Radix Sort trong việc sắp xếp dữ liệu

• Không phụ thuộc vào số lượng phép so sánh: Radix Sort không sử dụng các phép so sánh trực tiếp giữa các phần tử, do đó không phụ thuộc vào số lượng phép so sánh và không bị ảnh hưởng bởi phân bố ban đầu của dữ liệu. Điều này giúp nó có hiệu suất tốt khi sắp xếp các dãy số lớn.
• Hiệu quả với các dãy số có kích thước lớn: Radix Sort có hiệu quả tốt đối với các dãy số lớn, đặc biệt là khi các số có cùng độ dài chữ số. Với mỗi chữ số, thuật toán sẽ phân loại các số vào các thùng (buckets), giúp giảm đáng kể số lượng phép so sánh.
• Stablity (Ổn định): Radix Sort là thuật toán ổn định, nghĩa là nếu có hai phần tử bằng nhau, thứ tự của chúng trong dãy gốc sẽ được duy trì sau khi sắp xếp.

B. Hạn chế và trường hợp không nên sử dụng thuật toán Radix Sort

• Số lượng chữ số lớn: Radix Sort yêu cầu xác định số lượng chữ số của số lớn nhất trong dãy số để hoạt động hiệu quả. Trong trường hợp các số có số lượng chữ số rất lớn, việc xác định và sắp xếp các thùng (buckets) có thể tốn nhiều thời gian và bộ nhớ.
• Phạm vi giá trị dữ liệu: Radix Sort chỉ thích hợp cho các trường hợp phạm vi giá trị dữ liệu không quá lớn. Nếu các số trong dãy có giá trị rất lớn, có thể gây ra tràn số hoặc tiêu tốn nhiều bộ nhớ.

C. So sánh hiệu suất với các thuật toán sắp xếp khác

• So sánh với thuật toán QuickSort: QuickSort là một trong những thuật toán sắp xếp nhanh nhất và thường có hiệu suất tốt đối với các dãy số lớn và ngẫu nhiên. Tuy nhiên, Radix Sort có hiệu suất ổn định hơn khi dữ liệu sắp xếp đã gần gũi hoặc khi sắp xếp các dãy số có cùng độ dài chữ số.
• So sánh với thuật toán MergeSort: MergeSort có độ phức tạp thời gian ổn định và hoạt động hiệu quả trên các dãy số lớn và đã gần gũi. Tuy nhiên, khi dữ liệu có số lượng chữ số nhất định, Radix Sort có thể vượt trội hơn do không phụ thuộc vào số lượng phép so sánh.
• Radix Sort thường được ưu tiên sử dụng khi sắp xếp các dãy số lớn và có số lượng chữ số nhất định, đặc biệt là trong các trường hợp dữ liệu đã gần gũi. Tuy nhiên, nếu dữ liệu có giá trị rất lớn hoặc số lượng chữ số rất khác nhau, các thuật toán sắp xếp so sánh như QuickSort và MergeSort có thể hiệu quả hơn.

Lời kết

Thuật toán Radix Sort trong JavaScript là một công cụ mạnh mẽ để sắp xếp dữ liệu một cách hiệu quả và nhanh chóng. Khả năng sắp xếp từng chữ số của Radix Sort và hiệu suất tối ưu khiến nó trở thành một lựa chọn ưu việt trong việc giải quyết các vấn đề sắp xếp dữ liệu phức tạp.

Từ việc triển khai đến hiểu sâu về cơ chế hoạt động, bài viết này hy vọng đã giúp bạn hiểu rõ hơn về thuật toán Radix Sort và sự đóng góp của nó vào việc tối ưu hóa ứng dụng của bạn. Hãy tận dụng kiến thức này để xây dựng những ứng dụng mạnh mẽ và hiệu quả hơn, và khám phá thêm những khả năng mới mẻ của lĩnh vực sắp xếp dữ liệu trong lập trình.